AI从入门到放弃 BP神经网络算法推导及代码实现笔记，数据库与计算机网络服务

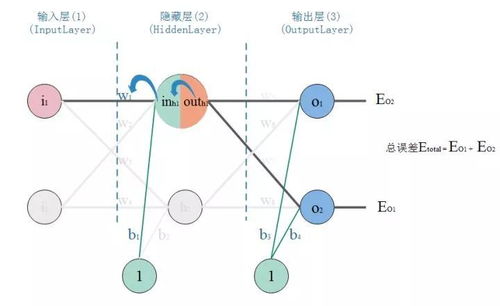
在人工智能的学习道路上，BP（Backpropagation）神经网络是一个关键节点，它结合了算法推导和实际代码实现，同时离不开数据库和计算机网络服务的支持。本文将从入门角度逐步推导BP神经网络算法，提供Python代码实现示例，并讨论数据库和网络服务在AI应用中的角色，帮助读者避免‘从入门到放弃’的陷阱。\n\n### 一、BP神经网络算法推导\nBP神经网络是一种多层前馈网络，通过误差反向传播算法进行训练。其核心包括前向传播和反向传播两个过程。\n\n1. 前向传播：输入数据从输入层经过隐藏层传递到输出层，计算各层神经元的输出。设输入向量为 \( x \)，隐藏层输出为 \( hj = f(\\sumi w{ij} xi + bj) \)，其中 \( f \) 是激活函数（如Sigmoid或ReLU），\( w{ij} \) 是权重，\( bj \) 是偏置。输出层类似计算得到预测值 \( yk \)。\n\n2. 反向传播：根据预测值与真实值的误差，反向调整权重和偏置。误差函数常用均方误差：\( E = \\frac{1}{2} \\sumk (yk - tk)^2 \)，其中 \( tk \) 是目标值。通过链式法则计算误差对权重和偏置的梯度：\n - 输出层梯度：\( \\frac{\\partial E}{\\partial w{jk}} = (yk - tk) \\cdot f'(netk) \\cdot hj \)，其中 \( netk \) 是输出层净输入。\n - 隐藏层梯度：类似计算，误差从输出层反向传播。\n 然后使用梯度下降法更新参数：\( w{ij} = w{ij} - \\eta \\frac{\\partial E}{\\partial w{ij}} \)，其中 \( \\eta \) 是学习率。\n\n推导的关键在于理解链式法则和激活函数的导数，例如Sigmoid函数 \( f(x) = \\frac{1}{1 + e^{-x}} \) 的导数为 \( f'(x) = f(x)(1 - f(x)) \)。\n\n### 二、代码实现示例（Python）\n以下是一个简单的BP神经网络实现，使用Sigmoid激活函数，适用于二分类问题。代码包括网络初始化、前向传播、反向传播和训练过程。\n\n`python\nimport numpy as np\n\nclass NeuralNetwork:\n def init(self, inputsize, hiddensize, outputsize):\n self.weights1 = np.random.randn(inputsize, hiddensize)\n self.weights2 = np.random.randn(hiddensize, outputsize)\n self.bias1 = np.zeros((1, hiddensize))\n self.bias2 = np.zeros((1, outputsize))\n \n def sigmoid(self, x):\n return 1 / (1 + np.exp(-x))\n \n def sigmoidderivative(self, x):\n return x * (1 - x)\n \n def forward(self, X):\n self.hidden = self.sigmoid(np.dot(X, self.weights1) + self.bias1)\n self.output = self.sigmoid(np.dot(self.hidden, self.weights2) + self.bias2)\n return self.output\n \n def backward(self, X, y, output, learningrate=0.1):\n error = y - output\n doutput = error * self.sigmoidderivative(output)\n errorhidden = doutput.dot(self.weights2.T)\n dhidden = errorhidden self.sigmoid_derivative(self.hidden)\n \n self.weights2 += self.hidden.T.dot(d_output) learningrate\n self.bias2 += np.sum(doutput, axis=0, keepdims=True) learning_rate\n self.weights1 += X.T.dot(d_hidden) learningrate\n self.bias1 += np.sum(dhidden, axis=0, keepdims=True) * learningrate\n \n def train(self, X, y, epochs=1000):\n for in range(epochs):\n output = self.forward(X)\n self.backward(X, y, output)\n\n# 示例使用\nX = np.array([[0, 0], [0, 1], [1, 0], [1, 1]]) # 输入数据\nY = np.array([[0], [1], [1], [0]]) # 目标输出（XOR问题）\n\nnn = NeuralNetwork(2, 4, 1) # 输入2个节点，隐藏层4个节点，输出1个节点\nnn.train(X, Y, epochs=10000)\nprint(\